Constructing FIR Digital Filters with valarray
Copyright © 2000 – Carlos Moreno
and Mochima Software/AudioSystems
Introduction
Digital filters are a fundamental tool in Digital Signal Processing (DSP) applications, and in general in data acquisition and processing applications. The uses of digital filters range from simple noise reduction to the complex spectral processing and analysis used in speech processing and recognition, audio, and communications.
A simplified definition of a digital filter is a system (software or hardware) that produces an output digital signal given an input digital signal, in which each sample of the output signal is obtained as a weighted average of a certain number of the previous input and output samples. In the case of FIR (Finite Impulse Response) filters, the output is a weighted average of the previous input samples only.
In this article, I present a C++ implementation of an FIR Digital Filters Library. The main focus of the article is the implementation, not the mathematical foundation and details about digital signals and DSP techniques. If you are not familiar with signal analysis and DSP theory, you can study the DSP reference shown at the end of the article [1], or any other books on DSP or Digital Filters.
FIR Digital Filters
Given an FIR filter described by a set of N coefficients {h[k]}, the value of the output signal at a particular time (i.e., the value of a particular sample of the output signal) is given by the following formula:
N-1
y[n] = SUM (x[n - k] * h[k]) (Eq. 1)
k=0
where x is the input signal, and y is the output signal. The operation described by Equation 1 is called convolution.
This convolution operation produces an output signal that is related to the input signal through a frequency response given by the following formula:
N-1
H(w) = SUM (h[n] * e-j*w*n) (Eq. 2)
n=0
where w is the normalized angular frequency, which must be between -pi and pi.
An example of a digital filter is the moving average, in which the output sample is the average of the last N input samples. This is an example of a low-pass filter (i.e., a filter that attenuates the high frequency components of the signal, which are related to abrupt changes and discontinuities in the signal). Figure 1 shows the effect of applying a moving average of the last five samples to reduce the noise for an input signal.
Equation 2 shows that given the filter coefficients, it is always possible to obtain the value of the frequency response (magnitude and phase) for a given frequency. The inverse process -obtaining the coefficients given a frequency response- is a far more complicated problem. Designing a digital filter is precisely the process of finding the coefficients given a frequency response specification. This problem has no exact solution in general. The filter designer usually tries to find a set of coefficients that closely match the specifications, while minimizing the effects of deviations with respect to the required frequency response.
Many methods exists for
the design of digital filters. In this article, I present an implementation
of the frequency sampling method, which in my opinion is the most straightforward
method. I also provide methods to directly initialize the coefficients of the
filter, so you can use other tools to design the filter, and then use this
implementation for the filtering processes in your applications.
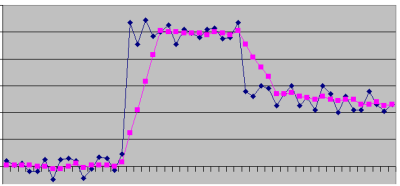 |
| Figure 1: Result of applying a moving average filter to a noisy input signal. Input signal is dark blue, output signal is purple. |
FIR Filter Class Definition
An FIR filter is described by a set of coefficients representing the impulse response of the filter (h). Mathematically speaking, these coefficients are usually real numbers. In practice, the particular application defines what is the best data type to represent the coefficients. For this reason, I provide a templatized representation for the FIR filter class, with a default type provided via a typedef:
Notice the use of the standard library valarray container. I chose to use valarray to represent the array of filter coefficients, given that the Standard suggests that compilers take maximum advantage of the numeric processing capabilities of processors and perform aggressive optimization techniques when using valarrays.
Constructors for Class basic_FIR
As I mentioned before, an FIR filter is described by an array of coefficients. However, the requirements for filtering applications are typically specified in terms of frequency response; designers must then use this frequency response to obtain the filter coefficients.
The constructors for class basic_FIR can be divided into two categories: initialization of filter objects given the values of the coefficients, and initialization given frequency response specifications.
In the first category, I provide two constructors: one that receives a valarray of coefficients representing the impulse response of the filter, and one that receives an array of coefficients plus a count of elements in the array (a C-like array of coefficients).
In both cases, the constructor's job is to copy the elements to the valarray h, inverting the order of the elements, as shown in listing 1 (FIR.h). The coefficients are stored in reverse order to accelerate the convolution operation, which will be performed once for each sample of the output signal.
In the second category, I provide several constructors that compute the filter coefficients given frequency response specifications. All these constructors use the frequency sampling method to obtain the coefficients for a linear phase filter design. The linear phase design implies that the impulse response of the filter is symmetric (i.e., h[k] = h[N-1-k] for 0 <= k < N, where N is the number of coefficients). Furthermore, I always provide an odd number of coefficients.
This linear phase design certainly imposes a limitation, but it is a simple design technique and is perfectly useful in many applications. Also, remember that you can always use any other design technique or filter design software to obtain the coefficients and use those values in your code to directly initialize the coefficients of the filter.
Listing 1 (FIR.h) and listing 2 (filter_types.h) show the details of these constructors. I use three auxiliary structure definitions to provide a convenient syntax to describe the standard filters, which are low-pass, high-pass, and band-pass. These structures contain the following information: cutoff frequency, sampling frequency, and number of frequency samples or constraint points. (The number of filter coefficients is equal to twice this number minus one).
These structures allow for clear and convenient expressions to create filter objects, as the following examples show:
A digital filter's coefficients are independent of the sampling frequency and the actual cutoff frequency. The only thing that determines the value of the coefficients is the ratio between the cutoff frequency and the sampling frequency. However, users of this class can conviniently specify the filters with the actual values from the specifications, without having to compute normalized angular frequencies.
Class basic_FIR provides two additional constructors, allowing you to initialize the filter object with a function specifying the frequency response, or a vector of frequency samples. In the first case, the constructor receives a pointer to a function taking a single double argument and returning a double. In the second case, the constructor receives a vector of Constraint_point structures, which are simple frequency/gain pairs. Listing 1 shows the implementation of these constructors. For both these constructors you must provide frequency specifications in terms of normalized angular frequency.
The frequency sampling method requires solving a set of linear equations, for which I use the Gauss method combined with a Matrix class. I do not discuss the details of solving the equations in this article. You can download the code and see the details or even modify it to use the matrix processing software of your choice.
Querying a basic_FIR for Frequency Response
Class basic_FIR also provides a method named H to obtain the value of the frequency response (H(w)) at a given normalized angular frequency. This member function returns an std::complex<double> value. You can obtain the magnitude using the complex type's abs() function, and the phase using its arg() function. Listing 1 shows the definition of the H member function.
Filtering Data with Filter Objects
Class basic_FIR includes two methods to perform filtering on a sequence of data. The first method computes a single sample of the output signal at a particular position of the input signal (that is, the output which corresopnds to a particular sequence of input samples, the last of which is the most recent sample). This member function is called output.
The templatized member function output receives a pointer or a pointer-like object (e.g., an iterator) to the most recent input sample (the data being filtered) and a reference to the object that will hold the result. An example of using this function is shown below:
Listing 1 shows the definition of this member function. It uses the Standard library's inner_product function to compute the result, given that the values of the coefficients are stored in reverse order. It also uses the function convert(), which I supply to provide rounding in conversions from floating point to integer, or any other specific conversion requirements. Listing 3 (conversions.h) shows some of the overloaded versions of convert, and the template function for the default conversions.
The second method for performing filtering is based on the idea that filtering data can be seen as an operation applied to a sequence of data. Usually this data is a digitized signal, but it doesn't have to be. Class basic_FIR provides a templatized member function that overloads operator () and provides an STL-like method to apply a digital filtering process to an arbitrary linear sequence of data. This allows you to code expressions like the following:
Listing 1 shows the definition for the templatized operator() member function. It applies the method output to each sample in the sequence.
Representing Signals
Digital filtering entailsl a couple of inconveniences that class basic_FIR does not solve. First, since the filtered output is a weighted average of the past N samples, output values cannot be computed until at least N input samples have been received. To produce outputs at the very beginning of the filter operation, some pseudo-inputs having value zero must be provided. Furthermore, the discontinuity that occurs where the actual input signals begins may produce undesirable output values.
Second, and most importantly, the examples shown in the previous section assumed that the data samples were stored in consecutive memory locations; that is, the examples assumed there was no memory limitation, so that much input data as needed could be stored in linear fashion.
This assumption represents no problem if the amount of data to be filtered is small. But in many situations, particularly those involving real-time embedded systems, the two above mentioned limitations need to be addressed in a way preserves efficient execution.
In general, the way to solve the finite-storage problem is by storing the input data in a circular buffer. A circular buffer is sufficient because most applications need access to only a fixed number of the most recent input samples. Such a buffer can be implemented efficiently by defining an array with a size equal to a power of two; a circular access pattern is obtained by ANDing a linearly increasing subscript with an appropriate mask. The resulting computed offset remains always within the array. The following C example illustrates the idea:
This technique can be encapsulated to provide a convenient object-oriented solution that doesn't necessarily sacrifice run-time efficiency.
A Class to Represent Signals
Template class Signal encapsulates the ideas discussed in the previous section, providing a convenient array-like container that uses a valarray to store the data.
The constructor for Signal receives and stores the size of the buffer, which should be at least the number of most recent samples required by the filter. However, this constructor resizes the internal valarray to a length equal to the lowest number that is a power of two and is greater than or equal to the requested size. For example, if you declare a Signal of 200 samples, it will allocate 256 elements. The Signal constructor computes the required size, allocates the space, and stores the corresponding mask for the AND operation required for the subscripted element access. (The value of the mask is always the allocated size minus one).
The Signal class also includes a data member to store the position of the most recently added sample (recent_sample_pos).
Listing 4 (Signals.h) shows the definition and implementation of the template class Signal.
Accessing the Data in Signal Objects
Accessing samples of a Signal object requires an AND operation with a mask, since the data is stored in a circular buffer. To encapsulate this operation, class Signal provides definitions for random-access iterators (Signal<T>::iterator and Signal<T>::const_iterator), as well as subscripted read-only access to the samples.
Thus, you can deal with a Signal object in a manner similar to a standard array. You can use negative subscripts to access the past samples, or you can use iterators as pointers to a linear sequence of samples. You need to keep in mind, however, that only a limited number of the previous samples will be available.
Listing 4 shows the definition of the overloaded subscripting operator and the iterator classes.
To obtain the current (most recent) sample, you can use either subscripted access with subscript 0, or the member function most_recent_sample(). You can obtain an iterator to the most recent sample by calling the member function begin(). Also, for additional compatibility with the STL idioms, I provided a member function front() as an alias for most_recent_sample().
Class Signal also provides several member functions to insert samples. You can insert one sample to a Signal object with the stream insertion operator, as shown below:
You can insert an entire block of samples using the insert_block() member functions, as shown in this example:
Inserting a block of samples is much more efficient than inserting one sample at a time, since the signal object implements the operation as one or two copy operations (besides the fact that it avoids the overhead of calling a member function once for each sample).
Additionally, class Signal allows you to fade-in samples, to avoid a discontinuity at the first sample. Two methods are available, and may be specified in the constructor: linear or cosine-shaped fade-in. The member function fade_in() receives a sample and inserts it in a way similar to the stream insertion operator, except that it multiplies the sample by a factor (between 0.0 and 1.0) that increases with each sample inserted.
Listing 4 shows the implementation of the stream insertion operator, the insert_block(), and the fade_in() member functions.
Filtering the Data in a Signal Object
Filter objects can directly perform filtering operations using the data in a Signal object. However, this approach would be inefficient, since we would require repeated use of iterators to the signal (to correctly obtain the previous samples), which would likely prevent the compiler from optimizing the inner_product operation.
Class Signal provides a more efficient way of filtering its own data. It takes advantage of the fact that if the most recent sample is not close to the beginning of the array used as circular buffer, then the array can be treated as a linear buffer. In other words, if the actual position of the current sample (given by the data member recent_sample_pos) is greater than the length of the filter, then the filtering operation is performed using a simple pointer to the most recent sample. Using a pointer means that the compiler may be able to optimize the inner_product operation. Note that if the size of the buffer is much larger than the length of the filter, the increase in the speed of execution may be significant, given that in most cases the operation is done using pointers to linear sequences of data.
Listing 4 shows the details of these operations, performed by the member functions filtered_output() and filtered_block().
Concrete examples
I now show two concrete examples of using the basic_FIR and Signal classes. In the first example, I perform real-time filtering one sample at a time. The filtering code is in a function called OnAudioData(). The example assumes that this function is automatically called when there is input audio data available (you can think of this as a message to a call-back function, or an event procedure, or an interrupt handler). Furthermore, the example assumes that audio data can be read/written with the functions get_audio_sample and put_audio_sample:
In the second example, I show how to use the block manipulation and filtering capabilities to digitally oversample a signal at four times its rate (say, from a sampling rate of 11.025 kHz to 44.1 kHz). I perform the oversampling operation as follows: 1) I insert one sample from the input (low rate) signal every four samples, 2)fill the rest of the samples with zeroes, and 3)apply a very sharp low-pass filter at the original frequency, which corresponds to the maximum frequency component of the input signal normalized with respect to the new (higher) sampling rate.
This example assumes the same conditions as the first example; furthermore, it assumes that audio can be read and written at different sampling rates with the functions get_audio_sample_block() and put_audio_sample_block().
This code could be simplified -- sacrificing efficiency -- to read one sample at a time and process blocks of 4 samples (the input sample plus the three padding zeroes):
Performance Measurements
Table 1 shows the results of a simple benchmark to evaluate the performance of the basic_FIR and Signal classes. The test consists of an oversampling to eight times the original sampling rate (similar to the example shown in the previous section). The signal consists of one hundred thousand samples, which means that the test involves filtering eight hundred thousand samples. A timer is used to measure the duration of the filtering process, including the time that it takes to copy data from the source to the Signal object, and the time that it takes to copy filtered data to the output buffer.
The results show the performance of the block processing and the one-sample-at-a-time processing, and compares the results with a C implementation that performs the filtering using linear blocks of memory (two arrays of eight hundred thousand elements). Two types of filters were used: one with int coefficients, and one with double coefficients. The application was run on a PII-233 machine with 128 MB of memory, working in Win32 console mode. The code was compiled with Visual C++ 6 using the /G5 /02 switches (to optimize for maximum speed using Pentium instructions).
The code used in this test is distributed with the rest of the source code that you can download from CUJ's ftp site. The files are called benchmark.cpp and benchmark.c.
The results show only a
slight advantage in the C approach, which I assume is due to the fact that
it uses linear memory storage (an unrealistic advantage) rather than any possible
overhead or ineficiency in the C++ implementation.
| Table 1: Time required for the filtering of 800,000 short int samples with a filter of 47 coefficients (in seconds) | ||
|
int
coefficients
|
double
coefficient
|
|
| C++ Block Processing |
0.89
|
1.49
|
| C++ Sample at a time |
2.98
|
13.31
|
| C Block Processing |
0.79
|
1.37
|
Conclusions
Digital Filters are a useful and powerful tool in signal and data processing applications. FIR digital filters provide a wide range of frequency response curves with good phase characteristics. In particular, FIR filters can be designed to exhibit linear phase response, which may be important in applications where control over the timing of the filtered signals is important, such as Active Noise Reduction or 3-D sound simulation.
The C++ implementation presented in this article provides a convenient, object-oriented way of applying FIR digital filtering techniques. Although I tried to provide as efficient an implementation as possible in terms of speed of execution, there is room for improvement. In particular, the idea of processing blocks of data could be combined with fast convolution techniques to provide faster filtering operations. Fast convolution uses FFT (Fast Fourier Transform) techniques to process contiguous blocks of data. An implementation using fast convolution would be even faster if it was used in a platform that had hardware-based FFT facilities.
Depending on the application, other simpler optimizations could be performed, such as removing the subscript validation in the overloaded subscripting operator in class Signal, or avoiding the throw statements and compiling without support for exceptions.
References
[1] John G. Proakis
and Dimitris G. Manolakis. Digital Signal Processing Principles, Algorithms,
and Applications, 2nd Edition (Macmillan Publishing Company, 1992).
[2] Bjarne Stroustrup. The C++ Programming Language, 3rd Edition (Addison-Wesley,
1997).
[3] Matthew H. Austern. Generic Programming and the STL (Addison-Wesley,
1999).
|
|